Simulation of NC tape preparation.
Problem Statement
A computer services company prepares computer numerical control part program tapes for metal-cutting manufacturing industries. Drawings of components are supplied by the manufacturers. A part programmer studies the drawings, and writes a part program manuscript to control the machine tool in cutting the workpiece. The programming takes 90 minutes, exponentially distributed. The manuscript is then typed onto a computer file, processed, and a tape is punched for the computer numerical control machine tool. This process takes 60 minutes on average, exponentially distributed. The tape is then loaded onto an appropriate machine tool for testing and editing. This process takes 70 minutes, exponentially distributed.
The computer services companys policy is to provide a fast, reliable service to industry. The company wishes to test several queuing disciplines for the processing of orders for the best overall service to customers.
Three possible disciplines of processing waiting jobs have been proposed.
1. First, process those jobs which have the shortest overall processing time.
2. First, process those jobs which have the longest overall processing time.
3. First, process the jobs which have the shortest due-date i.e. those jobs which are required soonest.
The flowtime for jobs is the total processing times (P4=P1+P2+P3), plus 3±1 days. The due-date is the relative clock time when the job arrives plus the allowed flow-time. Lateness is defined as the relative clock time when the job is completed, minus the due-date.
Simulate the processing of 100 orders by the computer services company.
1. Investigate the shortest processing time queue discipline.
2. Find the utilization of the facilities of manuscript writing, tape preparation, and editing.
3. Tabulate the lateness of orders and their transit times.
Listing
; GPSS World Sample File -
TAPEPREP.GPS, by Gerard F. Cummings
*********************************************************************
* *
* Computer Numerical Control *
* Tape Programming, Loading and Editing *
* *
*********************************************************************
* Queue Discipline Shortest Processing Time (SPT)
*********************************************************************
* P1 = Process Time for Programming
* P2 = " " " Punching
* P3 = " " " Editing
* P4 = Shortest Processing Time
* P5 = Due Date
* P6 = Longest Processing Time
*********************************************************************
RMULT 66753
Schedparm EQU 4 ;Start with short time
; process first
Var1 VARIABLE P1+P2+P3
Var2 VARIABLE P4+AC1+RN1@160+80
Var3 VARIABLE 10000-P4
Lateness VARIABLE AC1-P5
Transit TABLE M1,100,100,20 ;Tabulate flow times
Late TABLE V$Lateness,-1000,200,20 ;Lateness
*********************************************************************
GENERATE (Exponential(2,0,120))
;Create new arrivals
ASSIGN
1,(Exponential(3,0,90) ;Programming time
ASSIGN
2,(Exponential(4,0,60)) ;Tape punching time
ASSIGN
3,(Exponential(5,0,70)) ;Tape load and edit time
ASSIGN
4,V$Var1 ;Total processing time
ASSIGN
5,V$Var2 ;Due date time in P5
ASSIGN
6,V$Var3 ;Longest processing time
LINK
Program,P$Schedparm,Wrte ;Overall Shortest
Wrte SEIZE Manuscript
ADVANCE
P1 ;Part
program time
RELEASE Manuscript
UNLINK
Program,Wrte,1 ;Unlink one xact
LINK
Tape,P$Schedparm,Punch ;Link into chain
Punch SEIZE Tapepunch
ADVANCE
P2 ;Punching
time
RELEASE Tapepunch
UNLINK
Tape,Punch,1 ;Unlink one xact
LINK
Edit,P$Schedparm,Loadedit ;Link into chain
Loadedit SEIZE Edit
ADVANCE
P3 ;Load and
edit time
RELEASE Edit
UNLINK
Edit,Loadedit,1 ;Unlink one xact
**********************************************************************
TABULATE Late
TABULATE Transit
TERMINATE
1 ;Job
leaves the shop
**********************************************************************
After the Functions, Tables, and Variables are defined, the model is composed of a single segment. Transactions represent jobs, in various stages of completion. Each Transaction tabulates its own completion time, then decrements the Termination Count.
The Table Transit is used to tabulate a histogram of job completion times, and the Table Late tabulates the completion time minus the scheduled time. A late job, completed after its scheduled time, will register a positive value in the Late Table. An early job will register a negative value.
The named value Schedparm is used to specify which parameter, and therefore which scheduling policy, is to be used.
Running the Simulation
To run the simulation and create a Standard Report,
CHOOSE File / Open
and in the dialog box
SELECT Tapeprep
and then
SELECT Open
Next, create the simulation.
CHOOSE Command / Create Simulation
then
CHOOSE Command / START
and in the dialog box, replace the 1.
TYPE
100SELECT OK
The simulation will end when 100 Transactions have entered the "TERMINATE 1" Block. This represents the completion of 100 tapes.
When the simulation ends, GPSS World writes a report to the default report file, Tapeprep.1.1. As discussed in Chapter 1, the Report extension will vary depending on saved simulations and previously existing reports. For our purposes, we will assume that this is the first time the simulation has been created and run giving an extension of 1.1.
This report will be automatically displayed in a window. If you close the window, you can reopen it by using the GPSS World File / Open in the Main Menu. Then you should choose Report in the "Files of type" drop down box at the bottom of the window. GPSS World reports are written in a special format. If you wish to edit the report, you will have to copy its contents to the clipboard and from there into a word processor. You will not be able to open the file directly in a word processor.
Discussion of Results
The shortest time first policy led to a mean completion time of 433.5 minutes. However, 70% of the jobs were late. Perhaps the method of assigning due times should be investigated.
The utilizations of the Facilities of manuscript writing, tape punching, and editing were 74%, 46%, and 65%, respectively.
Inside the Simulation
Let's now explore the ending condition of the simulation which generated the Standard Report above. If you are not at the end of the simulation, please Retranslate the model and run it again.
First, look at the average lateness.
CHOOSE Command / SHOW
and in the dialog box
TYPE
TB$LateNext, the standard deviation of lateness.
CHOOSE Command / SHOW
and in the dialog box
TYPE
TD$LateNow, lets open some graphics windows.
CHOOSE Window / Simulation Window / Table Window
and in the drop-down box in the dialog box
CLICK ON The Down Arrow at the Right End of the Box
CLICK ON TRANSIT
SELECT OK
This is the Table Window for the Transit Table which shows the distribution of job completion times.
CHOOSE Window / Simulation Window / Table Window
and in the dialog box you will see that LATE is the selected Table
SELECT OK
Now, we see the histogram of late times.
Lets open the Expression Window on some simulation values.
CHOOSE Window / Simulation Window / Expression Window
The Edit Expression Window opens. When you enter the value in the second box in this dialog box, you should place the mouse pointer in the small box and click once. Do not press [Enter] to go from the first to the second box as GPSS World then assumes that all values have been entered. You can, instead, use [Tab] to move from box to box. Now, in the dialog box for the Label field
TYPE
Clockand in the Expression field
TYPE
AC1CLICK ON View
and
CLICK ON Memorize
If we memorize all the expressions, we'll be able to close the window and open it again later with easy retrieval of all the values. Also if you save the simulation the values in the Expression Window will be saved with the simulation if they have been memorized. We're going to close this window and reopen it later so please memorize this expression and the ones that follow.
In the dialog box for the Label field replace the current value
TYPE
# Leftand in the Expression field, replace the current value
TYPE
TG1CLICK ON View
CLICK ON Memorize
Finally, lets keep track of the transactions on the Userchains.
In the dialog box for the Label field, replace the current value
TYPE
# on Chainand in the Expression field, replace the current value
TYPE
CH$TapeCLICK ON View
CLICK ON Memorize
SELECT OK
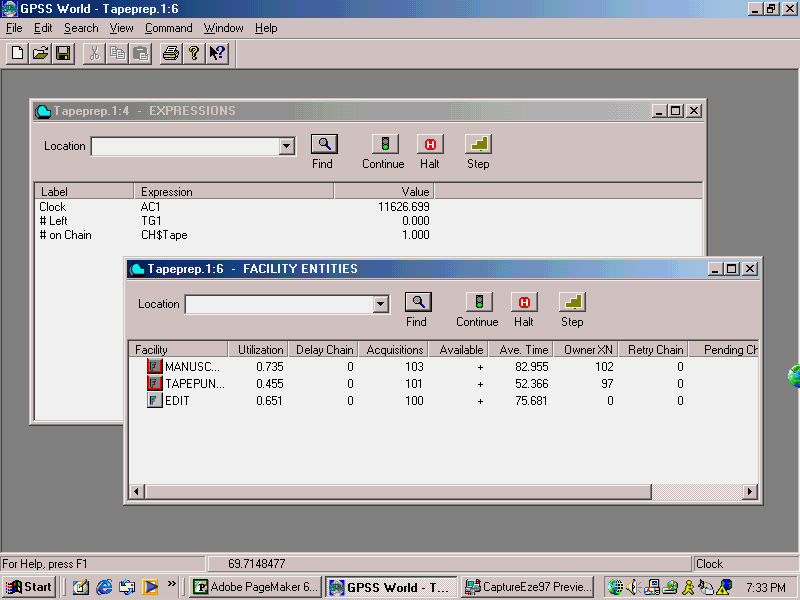
Lets run a short simulation, observing the Facilities and the values in the Expression Window. First, close all the other graphics windows that we are not going to observe. Make sure to leave open the Journal / Simulation Window.
CLICK ON The X-Upper Right of Each Window
CHOOSE Window / Simulation Window / Facilities Window
Open the Window to a comfortable viewing size and place it and the Expression Window so each can be seen.

Figure 161. Facilities and Expression Windows
Then,
CHOOSE Command / START
and in the dialog box, replace the 1.
TYPE
25,NPSELECT OK
When the simulation completes, close both windows.
CLICK ON The X-Upper Right of Each Window
It is a simple matter to shift the simulation to an earliest due date first policy. Notice that there are ASSIGN Blocks after the first GENERATE Block that put the various processing times into parameters. The named value Schedparm has been set equal to 4 which indicated the parameter to be looked at in order to know which scheduling policy to use. Lets use the due date policy this time.
CHOOSE Command / Custom
and in the dialog box
TYPE
Schedparm EQU 5SELECT OK
Then, use RESET to zero the statistics, but leave Transactions in the simulation. This will allow us to eliminate startup effects from the simulation. You should be sure when you do statistical comparisons with other runs that you have eliminated startup effects.
Now, from the Main Window menu,
CHOOSE Command / RESET
CHOOSE Command / START
and in the dialog box, replace the 1.
TYPE
100SELECT OK
Now, the average completion time for the new policy is given by
CHOOSE Command / SHOW
and in the dialog box
TYPE
TB$LateSELECT OK
Similarly, we can change to a longest process time first policy by changing Schedparm to equal 6 and resetting the statistics with a RESET, as we did above.
Before we report the results of these simulations, we must show that the observed effects are not due to random variation. The RESET and ANOVA Commands are provided for that purpose. They are discussed in Chapter 6 of the GPSS World Reference Manual.
Please feel free to modify the scheduling policy of the company, and simulate the effects. You may want to review the use of the LINK and UNLINK Blocks before you proceed.
Let's take a look at one final graphics window before we conclude this lesson. We'll view the Userchains. These are available to view in a Snapshot Window. When you first ran the model, at the end of the run, there were no transactions on the Userchains. At this point, we'll see some. We will expand the Chains only one level. You can expand them all the way if you wish by clicking on the additional plus signs.
CHOOSE Window / Simulation Snapshot / Userchains Window
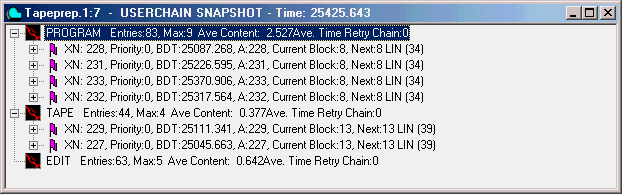
These chains represent the waiting lines for each of the three processes.
If you wish to go on to the next lesson, close all windows related to this model.
CLICK ON The X-Upper Right of Each Window
Otherwise, to end the session
CLICK ON The X-Upper Right of Main Window.
Simulation of traffic at a T-junction.
Problem Statement
Cars arrive at a T-junction every 6.28 seconds hyperexponentially distributed (standard deviation = 8.40 seconds). The cars then make a left turn northbound onto a highway. When cars cross the southbound lanes, they must wait in a center aisle which can accommodate a maximum of 8 cars. Each car takes 3.6 seconds (Erlang k=4 ) to cross the traffic lanes. It takes 4 seconds (Erlang k=5 ) to merge with northbound traffic. Southbound traffic arrives every 55±5 seconds and takes 15±5 seconds to pass the T-junction. Northbound traffic arrives every 60±5 seconds and takes 15±5 seconds to pass.
Simulate the traffic at the T-junction for 10 minutes.
1. Determine the transit time of northbound cars turning at the T-junction.
2. Tabulate the actual Erlang service times.
3. Find the maximum number of cars queuing in the lane, waiting to make a left turn.
Listing
; GPSS World Sample File -
TRAFFIC.GPS, by Gerard F. Cummings
***********************************************************************
* *
* Traffic at a T-Junction *
***********************************************************************
* Erlang Service Times ...Hyperexponential Arrivals *
* Time Unit is 1/100 Second *
***********************************************************************
* A Hyperexponential Probability Distribution Follows
Hyper FVARIABLE (410+((RN2L234)#(1343-410)))#(Exponential(2,0,1))
* f(t) = .234(1/4.10) exp(-t/4.1) + .766(1/13.43) exp(-t/13.43)
***********************************************************************
Aisle STORAGE 8
Mergetime TABLE MP2,100,100,20
Crosstime TABLE MP1,100,100,20
Transit TABLE M1,1000,1000,9
Arrivals TABLE V$Hyper,200,200,20
***********************************************************************
GENERATE V$Hyper,,300 ;Hyperexponential
QUEUE First
GATE SNF
Aisle ;Is there room in
the aisle?
SEIZE Southlane
;Crosses highway
DEPART First
MARK 1
*Erlang
Distribution
ADVANCE (Gamma(3,0,4,90)) ;Erlang
K=4 waiting time
*
;Mean = 360 time units
*
TABULATE Crosstime
;Record crossing time
ENTER
Aisle ;Stand in center
aisle
RELEASE Southlane
QUEUE
Two ;Queue for
northlane
SEIZE Northlane
DEPART Two
LEAVE Aisle
MARK 2
* Erlang
Distribution
ADVANCE (Gamma(4,0,5,80)) ;Erlang
K=5 waiting time
*
;Mean = 400 time units
*
RELEASE Northlane
TABULATE Mergetime
;Merge time to north flow
TABULATE Transit
TABULATE Arrivals
TERMINATE
***********************************************************************
GENERATE 5000,500,,,10
;Southbound traffic
SEIZE
Southlane
ADVANCE 1200,300 ;Time to
pass junction
RELEASE Southlane
TERMINATE
***********************************************************************
GENERATE 6000,500,,,10
;Northbound traffic
SEIZE
Northlane
ADVANCE
1200,300 ;Time to pass junction
RELEASE Northlane
TERMINATE
***********************************************************************
GENERATE
6000 ;Xact every minute
TERMINATE 1
***********************************************************************
There are 100 time units in a second. After the Functions, Tables, and Variables are defined, the model is composed of three segments. Transactions in the top segment represent traffic arriving at the T-junction, Transactions in the second segment represent southbound traffic on the highway, Transactions in the third segment represent northbound traffic on the highway, and Transactions in the bottom segment time the simulation by decrementing the Termination Count once per simulated minute.
Running the Simulation
To run the simulation and create a Standard Report,
CHOOSE File / Open
and in the dialog box
SELECT Traffic
and then
SELECT Open
Next, create the simulation.
CHOOSE Command / Create Simulation
then
CHOOSE Command / START
and in the dialog box, replace the 1.
TYPE
10SELECT OK
The simulation will end when 10 minutes of traffic has been simulated.
When the simulation ends, GPSS World writes a report to the default report file, Traffic.1.1. As discussed in Chapter 1, the Report extension will vary depending on saved simulations and previously existing reports. For our purposes, we will assume that this is the first time the simulation has been created and run giving an extension of 1.1.
This report will be automatically displayed in a window. If you close the window, you can reopen it by using the GPSS World File / Open in the Main Menu. Then you should choose Report in the "Files of type" drop down box at the bottom of the window. GPSS World reports are written in a special format. If you wish to edit the report, you will have to copy its contents to the clipboard and from there into a word processor. You will not be able to open the file directly in a word processor.
Discussion of Results
The transit times of northbound cars turning at the T-junction are tabulated in Table Transit. The average time was nearly 25 seconds. Times are in units of 0.01 seconds.
The actual Erlang service times were tabulated in Tables Crosstime and Mergetime. The crossing times had a mean of 3.63 seconds and a standard deviation of 0.39 seconds. The merging times had a mean of 4.05 seconds and a standard deviation of 0.47 seconds.
From the Queue Entity First we see that the maximum number of cars queuing in the lane, waiting to make a left turn was 8. The average time spent waiting was about 11.5 seconds.
Inside the Simulation
Let 's now explore the ending condition of the simulation which generated the Standard Report above. If you are not at the end of the simulation, please translate the model and run it again.
First, look at the average transit time.
CHOOSE Command / SHOW
and in the dialog box
TYPE
TB$TransitNext, the standard deviation of transit times.
CHOOSE Command / SHOW
and in the dialog box
TYPE
TD$TransitNow lets open some graphics windows.
CHOOSE Window / Simulation Window / Table Window
and in the drop-down box in the dialog box
CLICK ON The Down Arrow at the Right End of the Box
CLICK ON TRANSIT
SELECT OK
This is the Table Window for the Transit Table which shows the distribution of total times to travel through the intersection.
CHOOSE Window / Simulation Window / Table Window
and in the drop-down box in the dialog box
CLICK ON The Down Arrow at the Right End of the Box
CLICK ON CROSSTIME
SELECT OK
This is the Table Window which collects the times taken to cross the highway. If you wish, you may open the other Table Windows, MERGETIME, and ARRIVALS, in the same manner. When you are done looking at the various Table Windows, close them.
CLICK ON The X-Upper Right of Each Window
One way to watch the dynamics at the intersection is to view through the Facilities Window and the Storages Window.
CHOOSE Window / Simulation Window / Facilities Window
then
CHOOSE Command / START
and in the dialog box, replace the 1.
TYPE
1000SELECT OK
Now, we can see cars queuing for passage through the intersection. While the simulation is running, watch the delay chain for each Facility.
CHOOSE Window / Simulation Window / Storages Window
Now, we can see cars ready to turn.
When you are done observing the simulation, Halt it if it has not completed.
PRESS [F4]
If you wish to go on to the next lesson, close all windows related to this model.
CLICK ON The X-Upper Right of Each Window
Otherwise, to end the session
CLICK ON The X-Upper Right of Main Window.
Simulation of customer brand loyalty.
Problem Statement
A survey was carried out to assess the brand loyalty of customers to 7 brands of soap powder. The probability of change from one type of powder to another, is given in the table below. It is assumed that the customer will purchase either the same brand of powder again (most likely), or change to some other powder (less likely). Therefore the sum of the probabilities in each row of the matrix is equal to 1. The probability of the market share distribution depends on the number of transitions which have taken place (i.e. the number of successive purchases) and the initial market share of each product.
The purpose of the model is to estimate the market share each powder will achieve, in the long term, assuming that the transition probability matrix will remain the same, and assuming that initially all powders have an equal share of the market.
This process of system changes occurring in sequence is called a Markov Chain.
Probability of Customer Changing From Row to Column
SUDS BUBBLES CLEANPLUS
SOAPY
SUDS .39 .12 .17 .13 .10 .04 .05 1.0
BRANDX .13 .32 .10 .15 .12 .09 .09 1.0
BUBBLES .15 .14 .25 .14 .17 .08 .07 1.0
CLEARSHINE .11 .10 .09 .40 .08 .09 .13 1.0
CLEANPLUS .05 .12 .16 .09 .37 .14 .07 1.0
MARVEL .16 .13 .08 .05 .16 .28 .14 1.0
SOAPY .08 .10 .09 .10 .07 .13 .43 1.0
Since the table of transition probabilities has no zeroes, we know that all states are in a single chain, and are aperiodic. This assures the convergence of state probabilities in the theoretical Markov Chain, and assures that the simulation will not be trapped in a proper subset of states.
1) Run the model for 500 Transactions.
2) Determine the market share achieved by each product.
Listing
; GPSS World Sample File -
POWDER.GPS, by Gerard F. Cummings
***********************************************************************
* *
* Brand Loyalty by Customers *
***********************************************************************
RMULT 98851
Check TABLE X$Brand,1,1,8
*
Transitions MATRIX ,7,7 ;State transition table
*
Powder FUNCTION X$Brand,M7 ;Pick brand transition
1,FN$Suds/2,FN$BrandX/3,FN$Bubbles/4,FN$Clearshine
5,FN$Cleanplus/6,FN$Marvel/7,FN$Soapy
*
*
Suds FUNCTION RN1,D7 ;Transition from Suds
0.390,1/.510,2/.680,3/.810,4/.910,5/.950,6/1.0,7
*
BrandX FUNCTION RN1,D7 ;Transition from BrandX
0.130,1/.450,2/.550,3/.700,4/.820,5/.910,6/1.0,7
*
Bubbles FUNCTION RN1,D7 ;Transition from Bubbles
0.150,1/.290,2/.540,3/.680,4/.850,5/.930,6/1.0,7
*
Clearshine FUNCTION RN1,D7 ;Trans from Clearshine
0.110,1/.210,2/.300,3/.700,4/.780,5/.870,6/1.0,7
*
Cleanplus FUNCTION RN1,D7 ;Transition from Cleanplus
0.050,1/.170,2/.330,3/.420,4/.790,5/.930,6/1.0,7
*
Marvel FUNCTION RN1,D7 ;Transition from Marvel
0.160,1/.290,2/.370,3/.420,4/.580,5/.860,6/1.0,7
*
Soapy FUNCTION RN1,D7 ;Transition from Soapy
0.080,1/.180,2/.270,3/.370,4/.440,5/.570,6/1.0,7
*
Record FUNCTION X$Brand,L7 ;Records numbers
1,Suds/2,BrandX/3,Bubbles/4,Clearshine/5,Cleanplus/6,Marvel/7,Soapy
***********************************************************************
INITIAL X$Brand,1
GENERATE
1,,,,2 ;One xact every minute
TABULATE Check
SAVEVALUE Oldbrand,X$Brand
;Save old brand
SAVEVALUE Brand,FN$Powder ;Find
new brand
SAVEVALUE FN$Record+,1 ;Savevalue
of chosen brand
; up by one
MSAVEVALUE
Transitions+,X$Oldbrand,X$Brand,1 ;Update
TERMINATE 1
Running the Simulation
To run the simulation and create a Standard Report,
CHOOSE File / Open
and in the dialog box
SELECT Powder
and then
SELECT Open
Next, create the simulation.
CHOOSE Command / Create Simulation
then
CHOOSE Command / START
and in the dialog box, replace the 1.
TYPE
500SELECT OK
The simulation will end when 500 Transactions have entered the TERMINATE 1 Block. This represents 500 purchases.
When the simulation ends, GPSS World writes a report to the default report file, Powder.1.1. As discussed in Chapter 1, the Report extension will vary depending on saved simulations and previously existing reports. For our purposes, we will assume that this is the first time the simulation has been created and run giving an extension of 1.1.
This report will be automatically displayed in a window. If you close the window, you can reopen it by using the GPSS World File / Open in the Main Menu. Then you should choose Report in the "Files of type" drop down box at the bottom of the window. GPSS World reports are written in a special format. If you wish to edit the report, you will have to copy its contents to the clipboard and from there into a word processor. You will not be able to open the file directly in a word processor.
Discussion of Results
The approximate market shares are given in the Table Check. However, the results include startup effects.
Inside the Simulation
Let's now explore the ending condition of the simulation which generated the Standard Report above. If you are not at the end of the simulation, please Retranslate the model and run it again.
Now, lets open some graphics windows.
CHOOSE Window / Simulation Window / Table Window
and in the drop-down box in the dialog box CHECK is already selected.
SELECT OK
This shows the histogram representing market shares. Let 's now remove the statistics dependent on the startup conditions. In the Main Window menu,
CHOOSE Command / RESET
Now, continue the simulation for 100 more Transactions and suppress the Standard Report.
CHOOSE Command / START
and in the dialog box, replace the 1.
TYPE
100,NPSELECT OK
If we are truly at steady state conditions, you should not see any significant change in the market shares as the simulation runs. This means that although all columns in the histogram are growing, their relative sizes should not change significantly.
Close the Table Window.
CLICK ON The X-Upper Right of Table Window
Now, lets watch the dynamics of the model. Open a graphics window on the state transition matrix.
CHOOSE Window / Simulation Window / Matrix Window
and since TRANSITIONS is already selected in the drop-down box of the dialog box
SELECT OK
Now, continue the simulation for 100 more Transactions.
CHOOSE Command / START
and in the dialog box, replace the 1.
TYPE
100,NPSELECT OK
Each row in the matrix represents transitions out of any single state. Use the slide bar, if necessary, to see additional columns. Each column represents transitions into any single state. Every state change causes a cell in the transition matrix to be incremented.
If you wish to go on to the next lesson, close all windows related to this model.
CLICK ON The X-Upper Right of Each Window
Otherwise, to end the session
CLICK ON The X-Upper Right of Main Window.
Simulation of a solvable queuing network.
Problem Statement
When feasible, an analytical solution to queuing systems provides a useful means of estimating the performance of simple systems.
This program simulates a system for which the queuing parameters are calculated using the appropriate Pollaczek and Khintchin (P-K) equations. The objective is to verify the results obtained by simulation using GPSS World.
The program simulates an interarrival time of 5 seconds( 500 time units), exponentially distributed, and a single service channel. The mean service time is 3 seconds( 300 time units). The average utilization of the server is consequently 60%.
Three modes of service times are investigated.
1. Constant service time.
2. Exponentially distributed service time.
3. Erlang (k=2) service time.
1. Run the simulation for 500 minutes.
2. Determine the queue statistics for each type of service.
3. Compare the simulation results with the predictions of queuing theory.
Listing
; GPSS World Sample File - QTHEORY.GPS, by Gerard F. Cummings
**********************************************************************
* Queuing Theory Verification *
* Time Unit Is 1/100 Of a Second *
**********************************************************************
*
Transit TABLE M1,250,250,20
Number TABLE Q$Expon,0,1,20
Qconstant QTABLE Constant,200,200,20
Qexpon QTABLE Expon,200,200,20
Qerlang QTABLE Erlang,200,200,20
**********************************************************************
GENERATE (Exponential(1,0,500)) ;Interarrival 5 seconds
QUEUE Constant
SEIZE Facility1
ADVANCE 300
;Service constant 3 secs
RELEASE Facility1
DEPART Constant
TERMINATE
**********************************************************************
GENERATE (Exponential(1,0,500)) ;Interarrival 5 seconds
QUEUE Expon
SEIZE Facility2
ADVANCE (Exponential(1,0,300)) ;Service time 3 secs Expon
RELEASE Facility2
DEPART Expon
TABULATE Transit
TERMINATE
***********************************************************************
GENERATE (Exponential(1,0,500)) ;Interarrival time 5 secs
QUEUE Erlang
SEIZE Facility3
ADVANCE (Exponential(1,0,150)) ;Erlang K=2 Service 3 secs
ADVANCE (Exponential(1,0,150))
RELEASE Facility3
DEPART Erlang
TERMINATE
***********************************************************************
GENERATE (Exponential(1,0,6000)) ;Random sample,
; Ave. 1 per minute
TABULATE Number
TERMINATE 1
***********************************************************************
The model is organized into several segments. After the Storage Entities are defined and Savevalues initialized, there are three model segments for Transactions encountering Constant, Exponential and Erlang-2 service times, respectively.
Transactions in the bottom segment take random samples of the number of "exponential" Transactions in the system. These Transactions time the simulation and decrement the Termination Count once per simulated hour, on average.
Running the Simulation
To run the simulation and create a Standard Report,
CHOOSE File / Open
and in the dialog box
SELECT QTHEORY
and then
SELECT Open
Next, create the simulation.
CHOOSE Command / Create Simulation
then
CHOOSE Command / START
and in the dialog box, replace the 1.
TYPE
500SELECT OK
The simulation will end when 500 Transactions have entered the TERMINATE 1 Block. This represents 500 minutes of operation.
When the simulation ends, GPSS World writes a report to the default report file, Qtheory.1.1. As discussed in Chapter 1, the Report extension will vary depending on saved simulations and previously existing reports. For our purposes, we will assume that this is the first time the simulation has been created and run giving an extension of 1.1.
This report will be automatically displayed in a window. If you close the window, you can reopen it by using the GPSS World File / Open in the Main Menu. Then you should choose Report in the "Files of type" drop down box at the bottom of the window. GPSS World reports are written in a special format. If you wish to edit the report, you will have to copy its contents to the clipboard and from there into a word processor. You will not be able to open the file directly in a word processor.
Discussion of Results
The mean and standard deviations of queue time, queue length, and waiting time are calculated using the P-K formulae and tabulated below in table 1. Queue time is the sum of waiting time and service time. Results from GPSS World model QTHEORY.GPS are shown in parentheses.
Solutions Using Pollaczek and Khintchin Formulae Constant Exponential Erlang
Mean Queue Length
1.05 1.50
1.275
Mean Waiting Time
225 450
337.5
(Mean Queue Time - (226.7)
(453.5) (349.7)
Mean Service Time)
(Facility Ave. Time)
Std Dev Queue Time
319 750
415
(287) (739.9) (595)
Std Dev Queue Length 1.43 1.94 1.57
Std Dev Wait Time 130 276 195
For exponentially distributed service times, the probability of the number of Transactions in the system is calculated using the formula
P(n)=(1-l/m)(l/m)^n
where
l is the mean arrival rate, and m is the mean service rate. These probabilities are tabulated in Table 2. Results from the GPSS World model QTHEORY.GPS are shown in parentheses.
Table 2. Cumulative Probability of N Transactions in System
Number in System Cumulative QTHEORY.GPS
0 .4000 (.4060)
1 .6400 (.6320)
2 .7840 (.7740)
3 .8704 (.8660)
4 .9222 (.9160)
5 .9533 (.9560)
6 .9720 (.9660)
7 .9787 (.9820)
8 .9828 (.9840)
9
.9852 (.9960)
As the length of the simulation increases, the simulated values tend to approach the theoretical values. In the present case, we would normally run the simulation much longer to obtain more precision. This would cause our simulated results to converge to the theoretical values.
Lets observe the convergence to the average queue time for the exponential service time distribution. The theoretical value is 750 (7.50 seconds).
CHOOSE Window / Simulation Window / Table Window
and in the drop-down box in the dialog box
CLICK ON The Down Arrow at the Right End of the Box
CLICK ON Qexpon
SELECT OK
and
CHOOSE Command / Clear
SELECT OK
and
CHOOSE Command / START
and in the dialog box, replace the 1.
TYPE
10000,NPSELECT OK
When you are satisfied that the simulated result is converging toward the theoretical value (750), interrupt the simulation. Incidentally, the PLOT Window is useful for observing convergence, and for determining when startup transient effects are no longer significant. In your simulation projects, you will often want to exclude startup effects. Normally, you would enter a RESET Command to start the measurement period after startup effects had subsided.
If the simulation is still running, halt it now.
PRESS [F4]
If you wish to go on to the next lesson, close all windows related to this model.
CLICK ON
The X-Upper Right of Each WindowOtherwise, to end the session
CLICK ON The X-Upper Right of Main Window.
Simulation of a supermarket.
Problem Statement
Customers arrive by car to shop at a supermarket. The parking lot has space for 650 parked cars. If a customer fails to find a parking space, that customer leaves immediately without shopping. On average a customer can walk to the supermarket from the parking lot in 60 seconds. Shoppers purchase between 5 and 100 items, uniformly distributed. A customer buying 10 items or less, will generally use a basket (70 provided). A customer buying more than 10 items will generally use a cart (650 provided).
Shopping time per customer depends on the number of items purchased (10 seconds per item). Customers select items and then join the shortest queue at one of 17 checkouts. Customers purchasing less than 10 items may choose the express checkout. Checkout time takes 2 seconds per item purchased, plus a time of 25, 30, or 35 seconds. This time depends on the method of payment (cash, check or credit card which are assumed equally likely or probable). After checking out a customer walks to the car (60 seconds), loads goods and leaves the parking lot.
The arrival rate of customers is exponentially distributed, starting at 600 per hour for half an hour, 900 per hour for one hour, 450 per hour for one hour and 300 per hour thereafter.
1. Run the simulation for 3 hours.
2. Determine the transit time of customers.
3. Determine the utilization of the parking lot, carts, baskets and checkouts.
4. Tabulate the number of customers in the supermarket at one minute intervals.
Listing
; GPSS World Sample File -
SUPERMRK.GPS, by Gerard F. Cummings
***********************************************************************
* *
* Supermarket Simulation Model *
* Time Unit = 1/10 Of a Second *
***********************************************************************
RMULT 1187
First EQU 2
Last EQU 18
Qty VARIABLE (RN1@96+5)
Finance VARIABLE (RN1@3+1)#50+200
Transit TABLE M1,10000,10000,7 ;Time in system
Items TABLE P$Quantity,10,10,10 ;No. of items bought
Shoppers TABLE X$Customers,100,50,12 ;No. of shoppers
Baskt STORAGE 70
Cart STORAGE 650
Park STORAGE 650
Checkout VARIABLE (P$Quantity)#20+P$Payment
Tshop VARIABLE P$Quantity#100
INITIAL X$Customers,0
***********************************************************************
Beg TRANSFER Both,,Los ;Tries to park
or leaves
ENTER
Park ;Park in parking lot
ADVANCE
600 ;Time to walk from car
SAVEVALUE Customers+,1 ;One more
customer
ASSIGN
Quantity,V$Qty ;Param quantity = No. items bought
ASSIGN
Payment,V$Finance ;Param payment = Method
TEST LE
P$Quantity,10,Qcart ;Items >10 Get cart
GATE SNF Baskt,Qcart ;Check
basket available
QUEUE
Basket ;Queue for a basket
ENTER Baskt
;Get a basket
DEPART
Basket ;Leave queue
ASSIGN
Carrier,Baskt ;Param carrier assigned baskt
TRANSFER
,Shop ;OK to shop
***********************************************************************
Qcart QUEUE
Carts ;Queue for a cart
ENTER
Cart ;Get a cart
DEPART
Carts ;Depart carts queue
ASSIGN Carrier,Cart
;Param carrier assigned cart
Shop ADVANCE V$Tshop
;Shopping time elapses
TEST LE
P$Quantity,10,Norm ;Items < 10 go to express
COUNT L
Where,First,Last,1,Q ;Any empty checkouts?
TEST E
P$Where,0,Norm ;Some empty checkouts?
QUEUE Xpress
;Queue at express
SEIZE Xpres
;Get express checkout
DEPART Xpress
;Depart express queue
ADVANCE V$Checkout
;Checkout time
RELEASE Xpres
;Free express checkout
LEAVE
P$Carrier ;Leave the basket
TRANSFER ,Fin
***********************************************************************
Norm SELECT MIN Minque,First,Last,,Q ;Find minimum queue
QUEUE
P$Minque ;Join the min queue
SEIZE
P$Minque ;Get the checkout
DEPART P$Minque
;Depart the queue
ADVANCE V$Checkout
;Checkout time
RELEASE P$Minque
;Free the checkout
LEAVE
P$Carrier ;Leave the cart
Fin TABULATE Transit
;Record transit time
TABULATE
Items ;Record items bought
SAVEVALUE Customers-,1 ;One customer
leaves
ADVANCE
600 ;Walk to the car
LEAVE
Park ;Leave the car park
TERMINATE
Lost
TERMINATE
;One customer lost
***********************************************************************
* Arrivals for 0 - 30 min.
GENERATE
(Exponential(1,0,60)),,,300 ;A Customer
; arrives
TRANSFER ,Beg
* Arrivals for 30 - 90 min.
GENERATE
(Exponential(1,0,40)),,18000,900 ;Arrival rate
; after .5 hours
TRANSFER ,Beg
* Arrivals for 90 - 150 min.
GENERATE
(Exponential(1,0,80)),,54000,450 ;Arrival rate
; after 1.5 hrs
TRANSFER ,Beg
* Arrivals for 150 min +
GENERATE
(Exponential(1,0,120)),,90000 ;Arrival after
; 2.5 hours
TRANSFER ,Beg
***********************************************************************
GENERATE
600
;Xact each minute
TABULATE
Shoppers ;Record number of
customers
TERMINATE 1
***********************************************************************
The model is organized into several segments. After the
Variable Entities and Storage Entities are defined and Savevalues initialized,
there are three more model segments.
Transactions in the top segment represent customers who have arrived at the parking lot. If a Transaction finds that the Storage Entity named Park is full, the Transaction leaves the simulation. This represents a customer leaving without entering the store. Customers who enter the store acquire a cart or basket and proceed to shop. If the customer has more than 10 items, he/she joins the smallest checkout queue. The TEST Block in the third model segment performs this test, and sends any such Transactions to the Block labeled Normal. The minimum queue is determined by the SELECT Block in the fourth model segment, which puts the appropriate Queue Entity number into the Transactions parameter named "Minque".
For those Transactions with 10 items, or less, the COUNT Block in the third model segment checks GPSS Queue Entities numbered 4 through 20 for an empty checkout station. If none is found, the Transaction gets into line for the express checkout station.
The next to last segment contains several GENERATE Blocks which turn on and off at the appropriate times to vary the arrival rate. One could also use a single GENERATE Block with a function modifier which depends on the system clock. The Transactions in the bottom segment time the simulation; tabulate the number of customers at the end of each minute; and decrement the Termination Count.
Running the Simulation
To run the simulation and create a Standard Report,
CHOOSE File / Open
and in the dialog box
SELECT
Supermrkand then
SELECT Open
Next, create the simulation.
CHOOSE Command / Create Simulation
then
CHOOSE Command / START
and in the dialog box, replace the 1.
TYPE
180SELECT OK
The simulation will end when 180 Transactions have entered the TERMINATE 1 Block. This represents 3 hours of operation.
When the simulation ends, GPSS World writes a report to the default report file, Supermrk.1.1. As discussed in Chapter 1, the Report extension will vary depending on saved simulations and previously existing reports. For our purposes, we will assume that this is the first time the simulation has been created and run giving an extension of 1.1.
This report will be automatically displayed in a window. If you close the window, you can reopen it by using the GPSS World File / Open in the Main Menu. Then you should choose Report in the "Files of type" drop down box at the bottom of the window. GPSS World reports are written in a special format. If you wish to edit the report, you will have to copy its contents to the clipboard and from there into a word processor. You will not be able to open the file directly in a word processor.
Discussion of Results
From the Table Transit, we see that the average shopping time was 23641 seconds, or 394 minutes. From the Storage Entity subreport we see that the max content never reached the available capacity. Therefore, there were always enough parking places, baskets, and carts. However, a very large number of customers (397) are waiting in the checkout lines. They are, on average, spending more time waiting in line than they are shopping.
The Table Shoppers gives a histogram of customers in the supermarket, sampled at the end of every minute. There were, on average, 398.7 shoppers. Nearly all of these were waiting to check out.
Inside the Simulation
Now, let's now explore the ending condition of the simulation which generated the Standard Report above. If you are not at the end of the simulation, please Retranslate the model and run it again.
Lets use the SHOW Command to look at some System Numeric Attributes. These will be expressed in parts per thousand. First, the average utilization of baskets.
CHOOSE Command / SHOW
and in the dialog box
TYPE
SR$BasktNext, the utilization of carts.
CHOOSE Command / SHOW
and in the dialog box
TYPE
SR$CartNext, the utilization of parking places.
CHOOSE Command / SHOW
and in the dialog box
TYPE
SR$ParkThe easiest way to view these utilizations is to open the Storages Window.
CHOOSE Window / Simulation Window / Storages
This shows the Storage Entities representing the carts, baskets, and parking places. From the maximum in use, we see that none of these resources were exhausted during the simulation. The histogram of shopping times can be viewed next.
CHOOSE Window / Simulation Window / Table Window
and in the drop-down box in the dialog box
CLICK ON The Down Arrow at the Right End of the Box
CLICK ON TRANSIT
SELECT OK
You can also view the histograms of items purchased and shoppers in the supermarket. Those Tables are named Shoppers and Items.
Lets take a look at where Transactions are.
CHOOSE Window / Simulation Window / Blocks Window
Notice that many Transactions are in the QUEUE Block (Block 30) following the SELECT Block, waiting to enter a SEIZE Block. Transactions here represent customers trying to check out.
Lets turn now to the checkout lines.
CHOOSE Window / Simulation Window / Facilities Window
Use the slide bar on the side of the window to move to the Facility representing the express checkout line or make the window full screen.
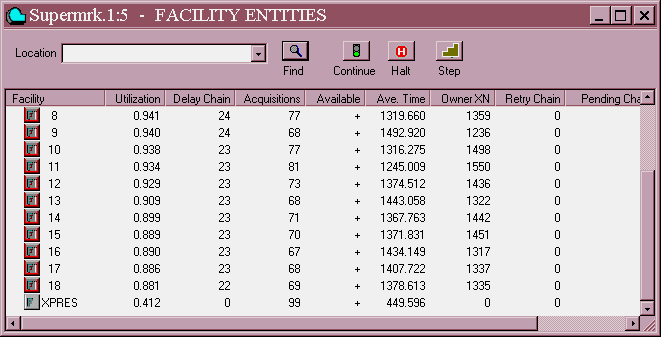
Figure 201. The Facilities Window showing the express checkout
Notice that all checkout stations are heavily utilized and have large queues except for the express checkout. Clearly, this situation must be avoided by the management of the supermarket. Before we go on lets close up the graphics windows that we have opened up until now.
CLICK ON The X-Upper Right of Each Window
Lets see if adding 10 more checkout stations will solve the problem. Go ahead and change the value of Last to 28. This increases the number of checkout lines from 17 to 27.
CHOOSE Command / Custom
and in the dialog box
TYPE
Last EQU 28SELECT OK
and
CHOOSE Command / CLEAR
Now, start the simulation running with the new number of lanes.
CHOOSE Command / START
and in the dialog box, replace the 1.
TYPE
180SELECT OK
When the simulation ends, look at the important statistics as before. Do you think 10 more checkout lines will suffice? Perhaps fewer would do. Management decisions such as the configuration of checkout lines are complex tradeoffs involving costs, revenues, and customer satisfaction.
Please feel free to modify the parameters and Blocks of this simulation.
If you wish to go on to the next lesson, close all windows related to this model.
CLICK ON The X-Upper Right of Each Window
Otherwise, to end the session
CLICK ON The X-Upper Right of Main Window.